Evaluating the privacy of PrivateSend

[Antti Kaikkonen]

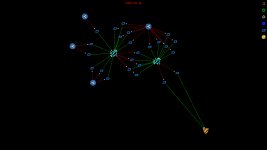
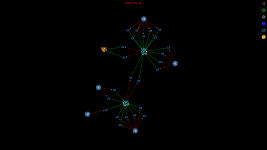
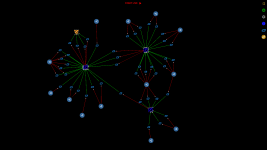
The goal of this project is to measure how private PrivateSend is

• for different number of rounds
• for different number of inputs in a PrivateSend transaction
  
• on average
• in the worst case (can we identify PrivateSend transactions with weak privacy)

How:

For a given PrivateSend transaction with k inputs

1. Find all paths from the PrivateSend transaction to all create denominations transactions that can be reached after a given number of mixing rounds
2. Find all k-combinations of paths such that in each combination the paths are not allowed to contain same transaction outputs
   
3. Now we have all possible mixing combinations for the PrivateSend transaction and we can start analysing the combinations.

Analyzing the combinations (examples):

• If we find zero combinations then we can conclude that the PrivateSend transaction didn't use the number of rounds we assumed
• If we have 1 combination then the PrivateSend transaction wasn't private for the assumed number of rounds (but it could be private for a different number of rounds)
• If we find that in all of the combinations one of the PrivateSend inputs always maps to the same create denominations transaction then the PrivateSend transaction wasn't private for the assumed number of rounds (but it could be private for a different number of rounds)
• We could also count the number of possible wallets for each of the PrivateSend inputs and use the minimum as a measure of how private the transaction was

I don't expect anyone to understand what I mean yet, but I'm planning to create some diagrams etc to help with that.

I have already completed step 1. I also created an algorithm for step 2, but I haven't tested it with real data yet. I think it will be possible compute all the combinations for a small number of rounds but it might be computationally infeasible if we have many inputs combined with for example 8 rounds.

 

[Antti Kaikkonen]

Today I decided to search the blockchain for privatesend inputs that can't be using more than 2 rounds. I found several such transactions.

Here are 3 examples:
1:

dashradar import json

2: Only 3 possible mixing sources (create-denominations transactions). Actually only 2 because there is only one connection to one of the create-denominations tx so the other PrivateSend input has to go to one of the two other ones.

dashradar import json

3:

dashradar import json

All the inputs of the mixing transactions in the images are expanded and there is no path to a 3rd round. Basically the first example has 4 possible create-denominations transactions. Second example has only 3 2 and the last example has 7.

The data in the json links can be imported to https://dashradar.com to reconstruct the graphs.

 

[jimbursch]

Today I decided to search the blockchain for privatesend inputs that can't be using more than 2 rounds. I found several such transactions.

@UdjinM6 -- can you evaluate what @Antti Kaikkonen is reporting?

 

[demo]

Today I decided to search the blockchain for privatesend inputs that can't be using more than 2 rounds. I found several such transactions.

Here are 3 examples:
1:
View attachment 6623
dashradar import json

2: Only 3 possible mixing sources (create-denominations transactions). Actually only 2 because there is only one connection to one of the create-denominations tx so the other PrivateSend input has to go to one of the two other ones.
View attachment 6622
dashradar import json

3:
View attachment 6621
dashradar import json

All the inputs of the mixing transactions in the images are expanded and there is no path to a 3rd round. Basically the first example has 4 possible create-denominations transactions. Second example has only 3 2 and the last example has 7.

The data in the json links can be imported to https://dashradar.com to reconstruct the graphs.

I was wondering, if you expand all graphs, is it possible to discover the recipient address of a privatesend transaction?

 

[Antti Kaikkonen]

I was wondering, if you expand all graphs, is it possible to discover the recipient address of a privatesend transaction?

PrivateSend does not hide the recipient address or amount. You can simply expand the outputs of a private send transaction to find the address.. Or
simply use a block explorer.

 

[jimbursch]

Hi @Antti Kaikkonen

I found your report in Bugcrowd and replied. My understanding is that 2 rounds of mixing, while weak for privacy, is a user's choice and does not pose a security risk. There may be use-cases where 2 rounds of mixing is adequate. But I could be wrong in my limited knowledge.

 

[Antti Kaikkonen]

Hi @Antti Kaikkonen

I found your report in Bugcrowd and replied. My understanding is that 2 rounds of mixing, while weak for privacy, is a user's choice and does not pose a security risk. There may be use-cases where 2 rounds of mixing is adequate. But I could be wrong in my limited knowledge.

Hi. I replied you in bugcrowd. Here is the same reply:

For a normal PrivateSend transaction input it is not possible to determine the number of rounds used just by analyzing the blockchain. However, in the examples I provided it was possible determine that no more than two rounds was used. This was caused by some of the mixing transactions having inputs only from create denominations transactions. As a result of knowing that the PrivateSend inputs were using only 2 rounds it is easy to determine all the possible mixing sources (only two in one of the examples). If there was paths to more mixing rounds, then someone analyzing the blockchain would have to assume 2-8 rounds were used and there would be multiple orders of magnitude more possible mixing sources. So even using only 2 rounds could be a lot more private than it currently is in some cases.

 

[Antti Kaikkonen]

In my opinion at least the user should receive a warning before sending if his/her PrivateSend transaction could be tracked to only two possible mixing sources.

 

[Antti Kaikkonen]

As I suspected, computing all the possible mixing combinations for a PrivateSend transaction is computationally really hard. For example I managed to do it for a privatesend transaction with 3 inputs using 4 rounds. That resulted in ~10 billion combinations and took something like 30 minutes using all 8 cpu cores of my computer. Analysing 5 rounds might already take years.

For that reason I developed a method which repeatedly generates random combinations and then analyses how many times different create denominations transactions are reached from each of the PrivateSend inputs.

I tested it on the PrivateSend transaction 59d51690d4b56ddbf1e393fa8d3a49bcfc3247f270f36be3b6ee411802666cba using 4 rounds and 1 million random combinations. Here is the result: https://pastebin.com/raw/sTemVnbY

1b8c10b8437102810650d1e35e639938218512919c5c53ba36e9f54cfce3e904 and 50b2089d6d0805b4699134f9d4a3f4c89e6d9f278cd9066e96a697e35eefe320 are the inputs to the PrivateSend transaction and the transaction ids below them are all create denominations transactions. The number after "=" is the probability of a PrivateSend input coming from that create denominations transaction. For example 0.12035 should mean that there is ~12% probability that it is one of the sources of that PrivateSend transaction.

 

[Antti Kaikkonen]

I changed the output format of the Monte Carlo simulation defined in the previous post.

The new output format simply lists txids of create denominations transaction and the probability that at least one of the privatesend inputs is originated from that transaction.

Here is the the result for 59d51690d4b56ddbf1e393fa8d3a49bcfc3247f270f36be3b6ee411802666cba with 4 rounds assumed: https://pastebin.com/zv2v8NhB

For example 911d8271516aab449dd108b002fe82e3757c2bf181040ee7718f088c871c96da=0.25711422641816556 means that 911d8271516aab449dd108b002fe82e3757c2bf181040ee7718f088c871c96da appeared in 25.71% of the one million randomly generated combinations.

I'm planning to implement "address clustering" a.k.a "guesstimated wallets" so that create denominations transactions belonging to the same wallet can be combined and the program could list the wallets and associated probabilities instead. I'm also planning to create a budget proposal to fund implementing all this in the dashradar website.

 

[Antti Kaikkonen]

I made two diagrams in an attempt to better explain what I'm doing.

In both diagrams I use an example of a PrivateSend transaction with 3 inputs: red, blue and orange. The remaining graph contains all the possible 2 round paths to PrivateSend create denominations transactions.

In the first diagram all 24 of the possible mixing combinations are displayed. In each combinations, multiple inputs are allowed travel through same mixing transaction, but they are not allowed to share common edges because that would mean that a single transaction output was spent twice. It is practically possible compute all the possible mixing combinations when the number of PrivateSend inputs is low and/or the number of mixing rounds analyzed is low.

The second diagram shows how it is possible to generate a single random mixing combination. This process can be quickly repeated a lot of times and then the randomly generated combinations can be analyzed to determine if the PrivateSend transaction is secure.

In this specific example both methods would come to the conclusion that the PrivateSend transaction is not secure if it used two rounds, because in all of the mixing combinations shown in the first diagram, there is at least one input mapped to the create denominations transaction in the middle.

 

[strophy]

Hi @Antti Kaikkonen I confess I don't fully understand the technicalities of what you are reporting, but I wonder if it is the same thing as was reported here:

https://arxiv.org/pdf/1709.02489.pdf

In Section 3.2 these guys describe a method for a cluster intersection attack on PrivateSend, is this similar to your method? Would this attack be practically possible against 2 rounds of mixing?

 

[Antti Kaikkonen]

Hi @Antti Kaikkonen I confess I don't fully understand the technicalities of what you are reporting, but I wonder if it is the same thing as was reported here:

https://arxiv.org/pdf/1709.02489.pdf

In Section 3.2 these guys describe a method for a cluster intersection attack on PrivateSend, is this similar to your method? Would this attack be practically possible against 2 rounds of mixing?

The cluster intersection attack would only consider the mixing combinations where all the mixing sources (create denominations transactions) are originated from the same address cluster. The address clusters a.k.a. guestimated wallets can be computed by using address clustering heuristics.

I believe that the cluster intersection attack can also produce false positives. For example if I mix a large amount of Dash from a single source address then it can easily be possible that all PrivateSend inputs of someone else's transaction can be traced back to that address.

In other words I believe that the cluster intersection method can provide circumstantial evidence at best. For example we might be able to say that:
if privatesend transaction "xyz" used 2 rounds and the mixing was originated from a single address cluster, then the address cluster containing addresses {a1, a2 ...} is the source. But if one of the two assumptions is wrong then that might not be the case.

 

[Antti Kaikkonen]

Update:

I made a demo website to demonstrate the PrivateSend analysis tool. Here is a few example PrivateSend transactions analyzed:

https://demo.dashradar.com/?txid=d055b2a298522124a6ad00acf03c280efdb0ace409ade2bff6ef4b4ff159a1f2
https://demo.dashradar.com/?txid=3b26a21ee041e5cafec3171d2bdc3e49252c12c9ae439ddf6f586bc30938aeb6
https://demo.dashradar.com/?txid=80e15776ed7e21158fc887d43bf85733017254bc196051a314df7412a2b6665f
https://demo.dashradar.com/?txid=e42a68729d9aaab4f11dfde7fd21a0c3c959e3dbaa9d3c64f5e406b568c199c7
https://demo.dashradar.com/?txid=ee30fb04d2526c7f02266ec83b6f95f2054456e6145ead532af9e92e587b1e73
https://demo.dashradar.com/?txid=8c62533b8aa604613905eada0c27a54d92f1bc9d97ffce183d894bb21051f8a1

It contains all 25250 PrivateSend transactions between blocks 500000 and 862348. Here is the full list of included PrivateSend transactions: list.

How to interpret the results:
For example in the 2 rounds tab of d055b2a29.. it says that the create denominations transaction f63bb317.. appeared in 100% of the randomly generated mixing combinations. This means that if the PrivateSend transaction used 2 rounds, then that create denominations transaction is almost guaranteed to be one of the mixing sources. But it is also possible that the PrivateSend transaction used more than 2 rounds (analyzed in other tabs). It is also possible that the PrivateSend transaction used a different number of rounds for different inputs (not included in the analysis). It is also possible that there exists a 2-round mixing combination that doesn't contain that create denominations transaction but it is so unlikely that it didn't appear in any of the 107017 simulations.

If the number of randomly simulated mixings is low then the results can be inaccurate. If it is 0 then that means that most likely the PrivateSend transaction didn't use that number of rounds for all inputs.


Currently there are many transactions with a low number of simulated mixings. That is because it takes a lot of processing to run the simulations for 25250 transactions and 7 different number of rounds and I have been only been able run them for ~24 hours using 8 cpu cores so far.

If you are a masternode and think that it is important to analyze the privacy of PrivateSend then please vote on my proposal: https://www.dashcentral.org/p/DashRadar-development-2

 

[AndyDark]

Update:

I made a demo website to demonstrate the PrivateSend analysis tool. Here is a few example PrivateSend transactions analyzed:

https://demo.dashradar.com/?txid=d055b2a298522124a6ad00acf03c280efdb0ace409ade2bff6ef4b4ff159a1f2
https://demo.dashradar.com/?txid=3b26a21ee041e5cafec3171d2bdc3e49252c12c9ae439ddf6f586bc30938aeb6
https://demo.dashradar.com/?txid=80e15776ed7e21158fc887d43bf85733017254bc196051a314df7412a2b6665f
https://demo.dashradar.com/?txid=e42a68729d9aaab4f11dfde7fd21a0c3c959e3dbaa9d3c64f5e406b568c199c7
https://demo.dashradar.com/?txid=ee30fb04d2526c7f02266ec83b6f95f2054456e6145ead532af9e92e587b1e73
https://demo.dashradar.com/?txid=8c62533b8aa604613905eada0c27a54d92f1bc9d97ffce183d894bb21051f8a1

It contains all 25250 PrivateSend transactions between blocks 500000 and 862348. Here is the full list of included PrivateSend transactions: list.

How to interpret the results:
For example in the 2 rounds tab of d055b2a29.. it says that the create denominations transaction f63bb317.. appeared in 100% of the randomly generated mixing combinations. This means that if the PrivateSend transaction used 2 rounds, then that create denominations transaction is almost guaranteed to be one of the mixing sources. But it is also possible that the PrivateSend transaction used more than 2 rounds (analyzed in other tabs). It is also possible that the PrivateSend transaction used a different number of rounds for different inputs (not included in the analysis). It is also possible that there exists a 2-round mixing combination that doesn't contain that create denominations transaction but it is so unlikely that it didn't appear in any of the 107017 simulations.

If the number of randomly simulated mixings is low then the results can be inaccurate. If it is 0 then that means that most likely the PrivateSend transaction didn't use that number of rounds for all inputs.


Currently there are many transactions with a low number of simulated mixings. That is because it takes a lot of processing to run the simulations for 25250 transactions and 7 different number of rounds and I have been only been able run them for ~24 hours using 8 cpu cores so far.

If you are a masternode and think that it is important to analyze the privacy of PrivateSend then please vote on my proposal: https://www.dashcentral.org/p/DashRadar-development-2

nice analysis!

 

[jeffh]

This is great work @Antti Kaikkonen !!

Looking forward to seeing what comes next out of. I wonder if there's any way to offload this process to the GPU from your CPU, would it not be better suited to the task?

 

[Antti Kaikkonen]

nice analysis!

Thanks!

This is great work @Antti Kaikkonen !!

Looking forward to seeing what comes next out of. I wonder if there's any way to offload this process to the GPU from your CPU, would it not be better suited to the task?

Thanks for the feedback. That thing has crossed my mind also but I have never done any GPU programming so I don't know if graph traversal type algorithms are possible to implement in a gpu.

I have been thinking of more ways to measure privacy of PrivateSend transactions. One of them is finding the smallest possible set of create denominations transactions in which at least one has to be a mixing source. For example it might be possible say that one of {create_denoms_1, create_denoms_2, ... create_denoms_n} has to be a mixing source without assuming anything about the number of rounds used. More transactions in the set is obviously means better privacy. I tried that method once and got to 11 create denominations transactions for a specific PrivateSend transaction, but it took too long before it could find a larger set or conclude that a larger set doesn't exist, so I gave up.

I will also be adding address clustering functionality so that some create denominations transactions belonging in the same wallet can be combined.

 

[Antti Kaikkonen]

Updated the analysis data on the demo website. Now each transaction has been analyzed for at least 70 seconds (10 for each round). Transactions still have varying number of simulations because it is slower to find valid PrivateSend mixings when there is a large amount of inputs or when the inputs have many common potential mixing transactions.

 

[Antti Kaikkonen]

I made some charts to see how the number of inputs in a given denomination affects privacy.

The series (0.01, 0.1, 1.0 and 10.0) represent privatesend transactions that contain inputs only from the specific denomination.

The y-axis (Traceability) is the average percentage of the most often appearing mixing source(create denominations transaction).

The x-axis is the number of inputs.

There is a lot of variance when the number of inputs is high because PrivateSend transactions that use only one denomination and have many inputs are quite rare.

Next I'm probably going to study how much it affects privacy if many PrivateSend inputs are from the same transaction or time period. I think that the privacy will be stronger for PrivateSend transactions where the inputs are many blocks apart from each other.

If you are a masternode then please vote on my proposal here!

 

[Antti Kaikkonen]

2-input PrivateSend transaction charts above. I would have expected PrivateSend transactions where both inputs are from the same block to have significantly worse privacy but that doesn't seem to be the case. Sometimes it is even the opposite. I guess there might be too little data to analyze 2-input transactions reliably.