BLS: Is it really that slow?

Optimizing BLS performance

BLS is not new in the cryptocurrency world, it’s actually being actively discussed since a few years already. It is however seen as too slow for a cryptocurrency, which is one of the reasons a lot of research is put into improving ECDSA (e.g. Schnorr). In the naive form, BLS is about a magnitude slower than ECDSA when it comes to signature verification, which would be problematic when blocks get larger and larger.

In this article, I will mostly concentrate on the performance of signature verification and show how BLS’s unique properties can be leveraged to increase the performance of BLS signature verification to a level that is more than acceptable. If you haven’t already, I would suggest to read my previous article about Secret Key Sharing and Threshold Signatures as it also describes some of the unique BLS properties.

Some numbers to start with

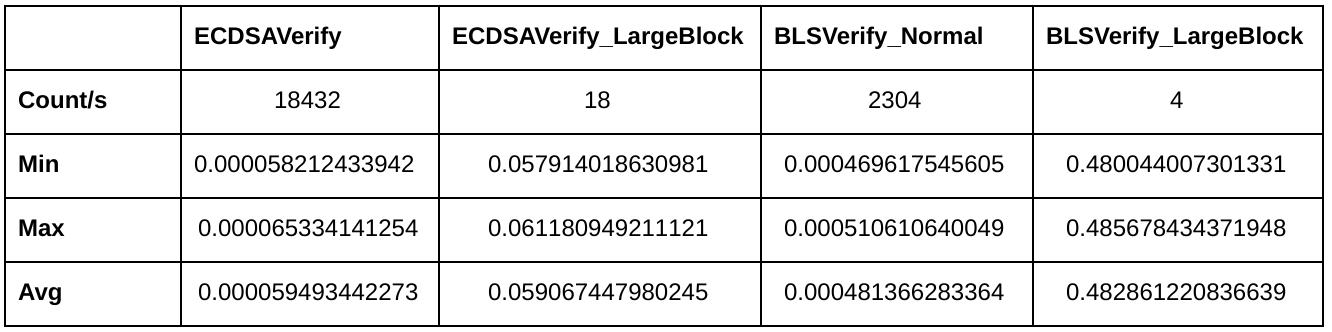
These numbers are copied from the internal Dash benchmark, where I’ve added a few simple benchmarks for ECDSA and BLS.

The ECDSAVerify benchmark simply performs as many verifications as possible in one second. The ECDSAVerifyLargeBlock kind of does the same, but it tries to verify 1000 signatures on each iteration instead of just one. A block with 1000 signatures is not really considered as a “large block”, but it’s a good number to work with. The benchmarks do not perform any additional verification like UTXO checks, it’s really just plain signature verification. All signatures, hashes and public keys are pre-calculated before the benchmark loop starts, so there is no unnecessary overhead inside the benchmarking loop.

The benchmark run shows us that a block with 1000 transactions would require around 60ms for signature verification if ECDSA is used. It’s around 482ms for a block with 1000 BLS signatures. Pretty bad if you look at this, right?

First optimization: Aggregation before Verification

Now let’s try to make the first and easiest optimization. It’s simply a pre-aggregation of all signatures in the block and then an aggregated verification. Aggregation is generally much faster than verification, so the overhead of this is negligible. The aggregated verification however still requires performing a lot of pairings (one per message hash, or transaction), so we still won’t get to an acceptable performance. Here are the numbers:

That’s 226ms for a block with 1000 signatures. It’s a significant improvement (more than 50% time saved), but it’s still not enough to compete with ECDSA.

This optimization depends on how BLS signatures would be stored in a block. If it would be identical to how it is done with ECDSA, we’d get the above numbers. If we however figure out how to properly aggregate BLS signatures as part of mining and thus store only a single aggregated signature in the block, the aggregation phase at validation time could be skipped. This would, however, only have a positive effect on the block size while the performance gained is really not worth mentioning.

Second optimization: Leverage mempool knowledge

Another form of this optimization has already been proposed when the discussions about BLS and Bitcoin started. The original proposal was to cache the results of the BLS pairings from transactions which are already in the mempool. Later, when a block is received, the aggregated verification would re-use the cached results internally instead of performing a fresh pairing.

The idea behind this is that a fresh block will mostly contain transactions which are already known by the receiving node. This is because propagation of transactions happens network-wide and thus each node should, in most cases, have received the transaction before a miner is able to mine it. If a transaction inside a new block is unknown by a node, it would however still have to perform the pairings for this transaction.

One of the developers who participated in the early BLS discussions announced at that time that he was working on this optimization. I contacted this developer and he told me that he was not able gain any significant performance improvements with this.

In the end, I didn’t try this optimization, but for a different reason. I believe there is a much better solution, which I’ll handle in the next section. Also, this optimization would require to implement a more complicated caching mechanism than the one used in ECDSA. This would also use much more RAM as intermediate pairing results (large numbers) would have to be stored in the cache.

Second optimization, part two

There is another solution that allows leveraging information from the mempool. Aggregation of BLS primitives is like multiplying two numbers, which means that division is also generally possible. This in turn means, that if we have an aggregated signature and we know the set of messages signed initially, we can simply divide the aggregated signature by the individual signatures of the known messages. If we do this, we can (actually, we must) omit the message hash and public key for this message when performing aggregated verification. The division of of signatures is significantly faster than the actual pairings involved in verification.

And if it’s not already clear: As fewer messages need to be verified for a given aggregated signature, less time is needed to verify the aggregated signature. The mempool of a node is a very good indicator of which signatures are already considered valid. A transaction will only be added to the local mempool if all signatures inside the transaction could be verified.

So, when a new block arrives which contains an aggregated signature, we can simply loop through all of the block’s transactions and for each transaction that is also in the local mempool, divide the block’s aggregated signature by the transaction’s signature. The final aggregated signature is then verified against the remaining (not found in mempool) transactions. Contrary to the previously described pairing-cache based optimization, this does not add additional complexity to the mempool or caches.

Performance improvements of this highly depend on how many of the globally propagated transactions are also in the node’s local mempool. This means, that after the node’s startup performance will very likely degrade for a few blocks, but then get faster and faster.

This is what the benchmark shows when 50% of the block’s transactions are locally known:

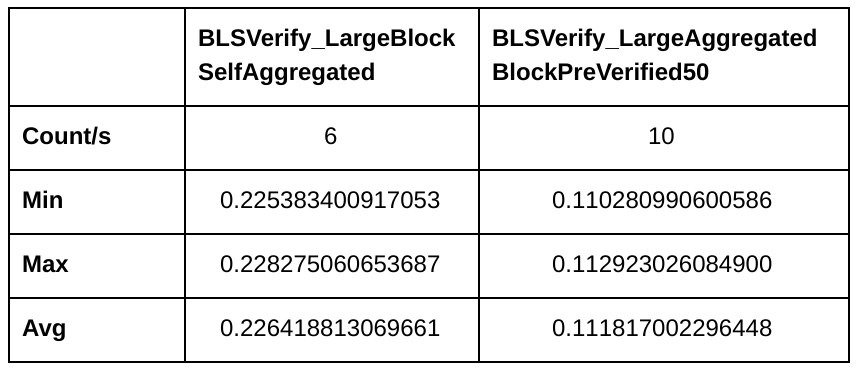
We’re down to 111ms for the block and we get closer to ECDSA’s performance 😉

Now with 90% transactions locally known:

Only 25ms now. Now we can compete with ECDSA’s 60ms.

These comparisons were unfair!

Yes, you’re right, these were unfair. I completely left out that the ECDSA verification performed in Dash and Bitcoin already does something comparable and simply skips verification of signatures which were already verified due to the mempool. So ECDSA performs a lot better than shown in my benchmarks. I still made that comparison because it seems to be assumed that such optimizations are not doable with BLS when signatures are aggregated in a block. Yes, we can’t naively re-implement the caching used by ECDSA verification, but we can come up with new solutions that better leverage the properties of BLS and in the end give the same improvements.

If I’d include a benchmark named ECDSAVerify_LargeBlockPreVerified, which simply skips 50% or 90% of all verifications, the speed improvements in ECDSA would approximately be 50% and 90%.

So in the 90% case, BLS has to compete with 6ms instead of 60ms. That’s 6ms ECDSA vs 25ms BLS, meaning that ECDSA is still around 5 times faster than BLS.

But, 25ms is still as acceptable as 6ms, simply because both numbers are too small to be noticed. Also, other things involved in block validation/processing require a lot more time, for example checking and updating the UTXO set, which involve a lot of slow disk access. Our limit is thus the time that is spent in parallel on disk related operations. As long as we don’t cross that limit, we’re fine. If more transactions would be involved, e.g. 10 times as much, our limit would also shift because all the other validation/processing would also require 10 times as much time.

Third optimization: Parallelization

All optimizations described so far do not take parallelization into account, meaning that multi-core systems are not leveraged. All of the proposed optimizations, including the aggregated verification, can be highly parallelized, which would give another significant performance improvement. A naive (but at least partly correct) way to take parallelization for block validation into account would be to divide all timings by the number of cores.

Fourth optimization: Batching

The optimizations described so far are only applicable to block validation. If transactions are received outside of a block, e.g. due to normal p2p propagation, the verification is reduced back to naive verification. But there are also ways to optimize this, for example by batching incoming transactions and then performing verification of multiple batches in parallel.

So, instead of immediately verifying an incoming transaction, a node could add new transactions to a pending batch. Only after enough transactions have been collected or after some timeout (e.g. 100ms) has passed, that pending batch is verified. Batch verification would than perform aggregated verification, which is basically the same as done in block validation.

If a batched verification fails, the node would have to fall back to naive verification for all signatures in the batch. This is because otherwise it wouldn’t know which of the transactions is the invalid one and thus know which ones to add to the mempool and which node to ban. Batch sizes should thus not be too large, as otherwise a single invalid transaction would dramatically slow down verification of a whole batch. The smaller the batch is, the less impact such a transaction has.

The interesting thing about this is, that the maximum throughput actually increases if transactions are received in a faster rate.

Here are some benchmarking results:

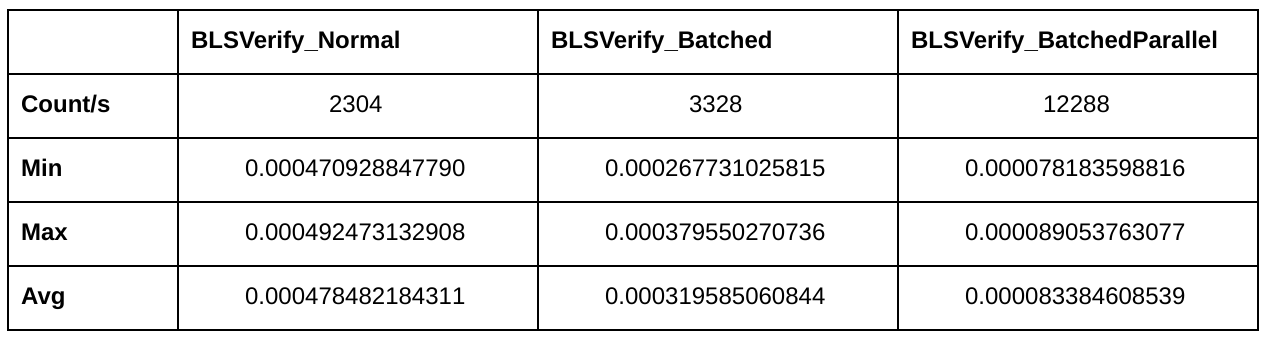
As you can see, batched verification alone already increases throughput by 44%. Together with parallelism (4 cores), the throughput is five times higher than with naive verification.

Worst case scenarios and why they’re not that bad

We must always consider worst case scenarios as this is what a possible attacker would target. For block validation, the worst case scenario is when the block includes a considerable amount of locally unknown transactions. In this case, performance would degrade to the numbers shown in the first optimization (aggregated verification only). This might happen in two cases. The first case is simply after startup of a node, as at that point the node’s mempool will be empty or outdated and thus the second optimization would not be leveraged. This situation however will fix itself after a short time, because the node will query other nodes for as many transactions as possible.

The second case in which this might happen is when a miner includes a large set of self-created transactions which he did not propagate to the network. In this case, a block with these transactions would become slow to propagate and poses a high risk of orphaning. If this would be done as part of an attack, it would require a very high amount of hashpower while at the same time risking losing of many block rewards. Miners are already now incentivized to only include transactions which are well propagated in the network, as already available optimizations (e.g. compact blocks or xthin) in block propagation are based on block-reconstruction instead of full transmission.

Additionally, a hostile node could try to send transactions to another node which degrade the batched verification of p2p transactions. Such transactions would however not be propagated further, simply because they are invalid. This means, that an attacker can only directly target a node. If an attacker would try this, he’d only have one attempt per available source IP, as invalid transactions result in banning of the IP. An attacker is thus unable to cause any significant damage.

Initial Block Sync

When doing the initial sync of the blockchain, or when catching up after being down for some time, the most important optimization, which is the second one, won’t work. This is because every transaction you encounter is a fresh one and thus no previously gathered knowledge can be leveraged.

The time required to verify all signatures in a block would match the numbers found in the first optimization. This would be 226ms per block of 1000 transactions. This scales linearly, so a 5x times increase in transactions requires 5x times as much time, so it would be 1.13s for 5000 transactions, which would be a block of around 1mb size (assuming 200 bytes per transaction).

This can also be highly parallelized, so assuming 4 cores, we’d reduce this to 0.283s per 1mb block. A full day worth of full 1mb blocks would require 2.7 minutes for verification. 32mb blocks would require 87 minutes per day. This would sum up to quite a lot long-term and thus is not acceptable on its own.

However, there is already functionality implemented in Bitcoin and Dash which reduces the impact of this; “the assumed valid block”. A user can specify a block hash with “-assumevalid=<hash>” at startup time. Each released version also includes an updated default value for this hash, which is agreed on and reviewed by multiple developers before release. Based on this value, the node will skip all script validation from blocks which are part of the same chain and before the given block hash. This dramatically speeds up validation of blocks, but only as long as not too much time has passed since the last release. Every block that appears after the release (after the default assumed valid block), will require full verification and thus will be as slow as described above.

To reduce the impact of slow verification, especially with BLS, we must find a way to update the default assumed valid block more often, without requiring a full release each time we do so. One possible solution would be to include a set of public keys in the node software and allow the node to query other nodes for the latest default assumed valid block hash. Only if the returned value is signed by a minimum number of keys, the node would then accept the value as the new default assumed valid block hash. The owners of the secret keys could then regularly (e.g. once every few days) sign an old enough block hash and propagate the signed value. This process could be fully automated as well. This however opens a few questions: Who are the persons having these keys? How many should it be? How can we trust them if no review of proposed values is done in advance? What’s the worst thing that can happen if enough people collaborate to sign a bad block hash?

Let’s answer the last question first. The worst thing that can happen is that validation while doing the initial sync gets slower for a node. The assumed valid block hash does not influence PoW rules and thus the value has no influence on which chain (if multiple exist) a node chooses to follow. If PoW rules result in another chain being followed than the assumed valid block, the node will fallback to full script verification. It is thus not possible to force a fork upon the network.

It is, however, theoretically possible to trick freshly synced nodes into syncing and accepting an invalid chain (as script verification was skipped). This is however only possible if the attacker has enough hash power to build a long-enough chain of invalid blocks up until the given assumed valid block and at the same time extend the invalid chain fast enough so that it can compete with the currently longest valid chain. As other nodes, which are fully synced since some time already, would have performed full validation on the invalid blocks a long time ago already, none of these other nodes would be following this invalid chain. This also includes other miners, meaning that other miners will continue mining on top of the valid chain and thus will eventually allow the attacked node to perform a chain reorganization and thus heal itself. Such an attack would be extremely expensive and unlikely to succeed. It’s basically the same as a 51% mining attack.

To sum it up; an attacker would need >=51% of hash power and at the same time would need to have control over the majority of keys used to sign the assumed valid block hash. If the attack is successful, only nodes which are currently syncing the chain (first start or multiple days downtime) would be affected. All other nodes, including other miners, the whole masternode network and all economically important nodes (e.g. exchanges), would simply reject the invalid chain. In the end, the attacker would only slow down a few nodes and then loose all the rewards he would have got if he would have been honest.

Now let’s handle the other questions, which mostly involve (lack of) trust. There are multiple options. For regular cryptocurrencies, the same people that already provided public keys for Gitian building could be used. These are mostly developers of the cryptocurrency or active contributors. It still involves too much trust in individuals, but as shown above these at least can’t seriously harm the network.

With masternode based cryptocurrencies like Dash, the masternodes itself can become signers of the assumed block hash value. As each masternode requires a collateral, the number of masternodes is limited by the circulating supply of a cryptocurrency, which makes sybil attacks impractical (which would be a problem if only regular nodes are available). This however requires that the list of available masternodes is verifiable before the full chain is available (as we are in initial sync), which will be possible in one of Dash’s next major releases. See this link for more details.

But why the hurdle?

You might ask, is this all worth it? I believe it is, because BLS gives us new opportunities and use cases which wouldn’t be possible with ECDSA only, or at least would be much harder to implement. The Secret Sharing and Threshold scheme presented in my previous blog post is one of these examples. Block-level aggregation is another example, as it would allow us to reduce most of the transactions signatures into a single 32 byte signature per block. Privacy can also be significantly improved with BLS, simply because it makes mixers more effective. There are also use cases related to consensus which leverage aggregated signature and/or threshold signatures. Generally, a lot of stuff that would be too expensive on-chain, will become reasonable to be put on-chain.

I also believe that simply using BLS instead of ECDSA makes large parts of SegWit unnecessary. It kind of solves the same problems (malleability and block space) while being easier to implement and at the same time allowing/improving many other things.

Conclusion

I believe that performance is not an issue if BLS would be used instead of ECDSA. The many advantages of BLS over ECDSA perfectly justify the small degradation of performance which is left after all the optimizations. The initial blockchain sync can also be improved, but requires more work and research. There is still more research and more experimentation required and I’m sure after some time, more and more optimizations, use-cases and general advantages will come to light.

There is still one thing which I did not handle. BLS and the involved pairings are much harder to prove being secure, compared to ECDSA. This is something I’m not able to give any meaningful contributions to, simply because I’m not deep enough in the math and cryptography topics. So far, it seems to be assumed secure, but research is still ongoing and I hope we’ll see some more big names in cryptography validating and proving the security of BLS.